Sinilausebash

Tässä postauksessa johdatellaan sinilausebashaukseen, eli miten sinilauseella voidaan laskennallisesti ratkaista geometrian tehtäviä.

Esitietoina oletetaan, että lukija tuntee tavallisimmat lukiossa esiintyvät trigonometriset manipulaatiot (summakaavat, Pythagoraan identiteetti, parillisuudet/parittomuudet, yms.). Sinilauseratkaisut perustuvat karkeasti ottaen laskennallisen suunnitelman tekemiseen ja sen toteuttamiseen. Tehtäväkohtaiset erot ovat kuitenkin suuria, minkä vuoksi kokemus on tärkeää. Kummempaa teoriaa ei tekniikkaan liity, minkä vuoksi käydään suoraan tehtäviin.

Esimerkkitehtäviä

MAOL, alkukilpailu, avoin sarja, 2012

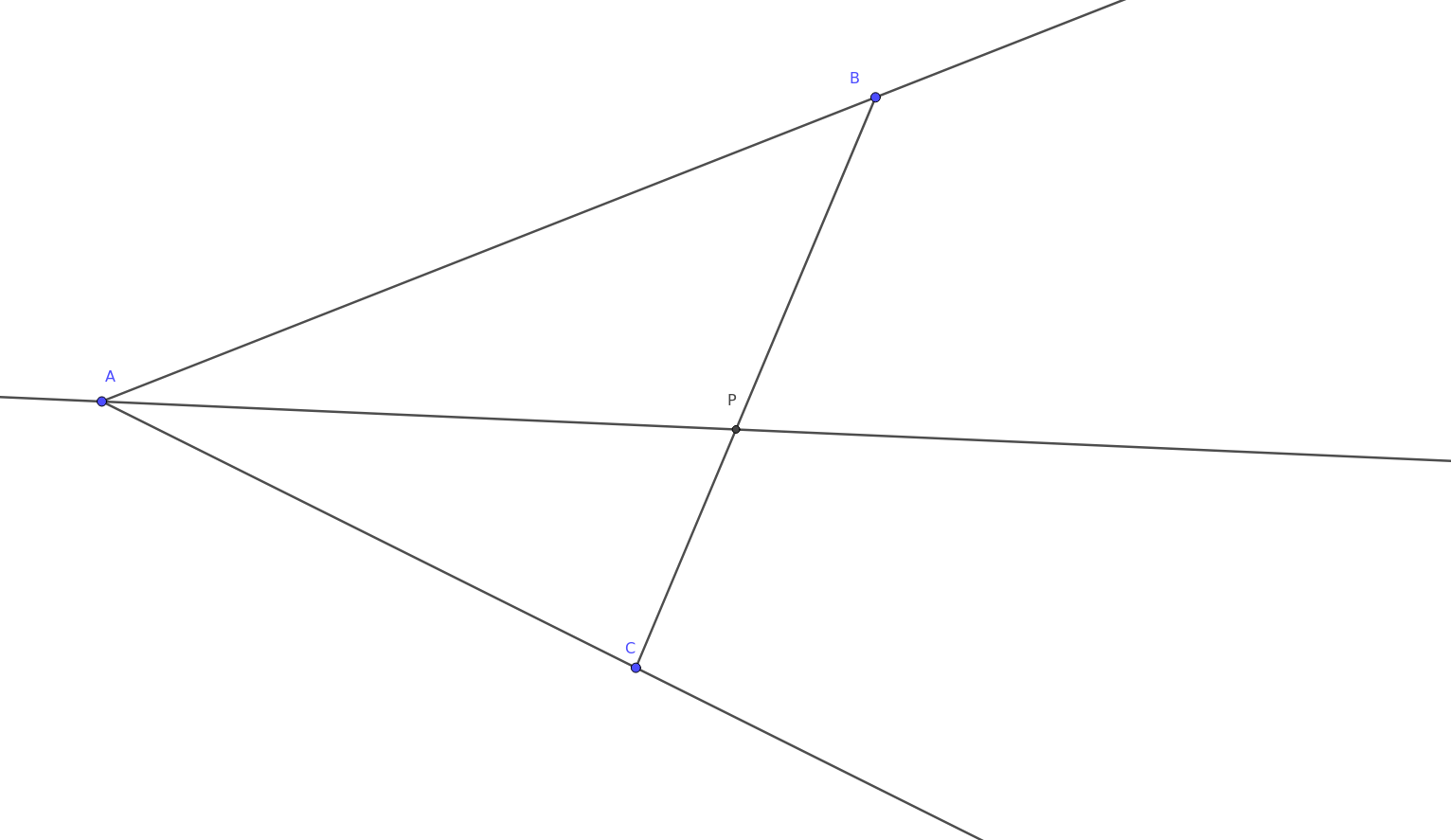
Terävän kulman $\angle A$ puolittajalta valitaan piste $P$ ja toiselta kyljeltä piste $B$. $BP$:n jatke leikkaa toisen kyljen pisteessä $C$. Osoita, että lausekkeen

$$\frac{1}{AB} + \frac{1}{AC}$$

arvo ei riipu pisteen $B$ valinnasta, kun $P$ pidetään paikallaan.

Ratkaisu

Suunnitelma on ilmoittaa suure $\frac{1}{AB} + \frac{1}{AC}$ joidenkin asioiden avulla, jotka ovat vakioita. Konfiguraatiossa vakioita ovat täsmälleen $\angle BAP, \angle PAC$ ja $AP$. Pyritään päätymään niihin.

Sovelletaan sinilausetta kolmioon $ABP$. Saamme

$$\frac{AB}{\sin(\angle APB)} = \frac{AP}{\sin(\angle ABP)}$$

Kertomalla ristiin saamme

$$\frac{1}{AB} = \frac{\sin(\angle ABP)}{\sin(\angle APB)} \cdot \frac{1}{AP}$$

Vastaavasti saamme $\frac{1}{AC} = \frac{\sin(\angle ACP)}{\sin(\angle APC)} \cdot \frac{1}{AP}$

Huomataan (varsin yleinen ja hyödyllinen sievennys), $\sin(\angle APC) = \sin(180^{\circ} - \angle APB) = \sin(\angle APB)$.

Siispä tutkittava summa muuttuu muotoon $\frac{1}{AB} + \frac{1}{AC} = \frac{1}{AP} \Big( \frac{\sin(\angle ABP) + \sin(\angle ACP)}{\sin(\angle{APB})} \Big)$

Koska haluamme osoittaa tämän olevan vakio, ei vakiotermistä $\frac{1}{AP}$ tarvitse murehtia. Kirjoitetaan yksinkertaisuuden vuoksi

$\angle BAP = \angle PAC = \angle A$, $\angle ABP = \angle B$, $\angle ACP = \angle C$ sekä $\angle APB = \angle P$.

Nyt näemme, että $\sin(\angle B) = \sin(180^{\circ} - \angle A - \angle P) = \sin(\angle A + \angle P)$.

Samaan tapaan $\sin(\angle C) = \sin(180^{\circ} - \angle A - (180 - \angle P)) = \sin(\angle P - \angle A)$.

Siis lauseke, jonka haluamme osoittaa olevan vakio, on nyt

$$\frac{\sin(\angle P + \angle A) + \sin(\angle P - \angle A)}{\sin(\angle P)}$$

Käytämme tähän sinin summakaavoja, ja huomaamme lopputuloksen riippuvan ainoastaan $\angle A$:sta, eli olemme valmiit.

.Baltian tie 2017, T12 Suora $l$ sivuaa ympyrää $S_1$ pisteessä $X$ ja ympyrää $S_2$ pisteessä $Y$. Piirretään suora $m$, joka on yhdensuuntainen suoran $l$ kanssa ja leikkaa ympyrän $S_1$ pisteessä $P$ ja ympyrän $S_2$ pisteessä $Q$. Osoita, että osamäärä $\frac{XP}{YQ}$ ei riipu suoran $m$ valinnasta.

Ratkaisu

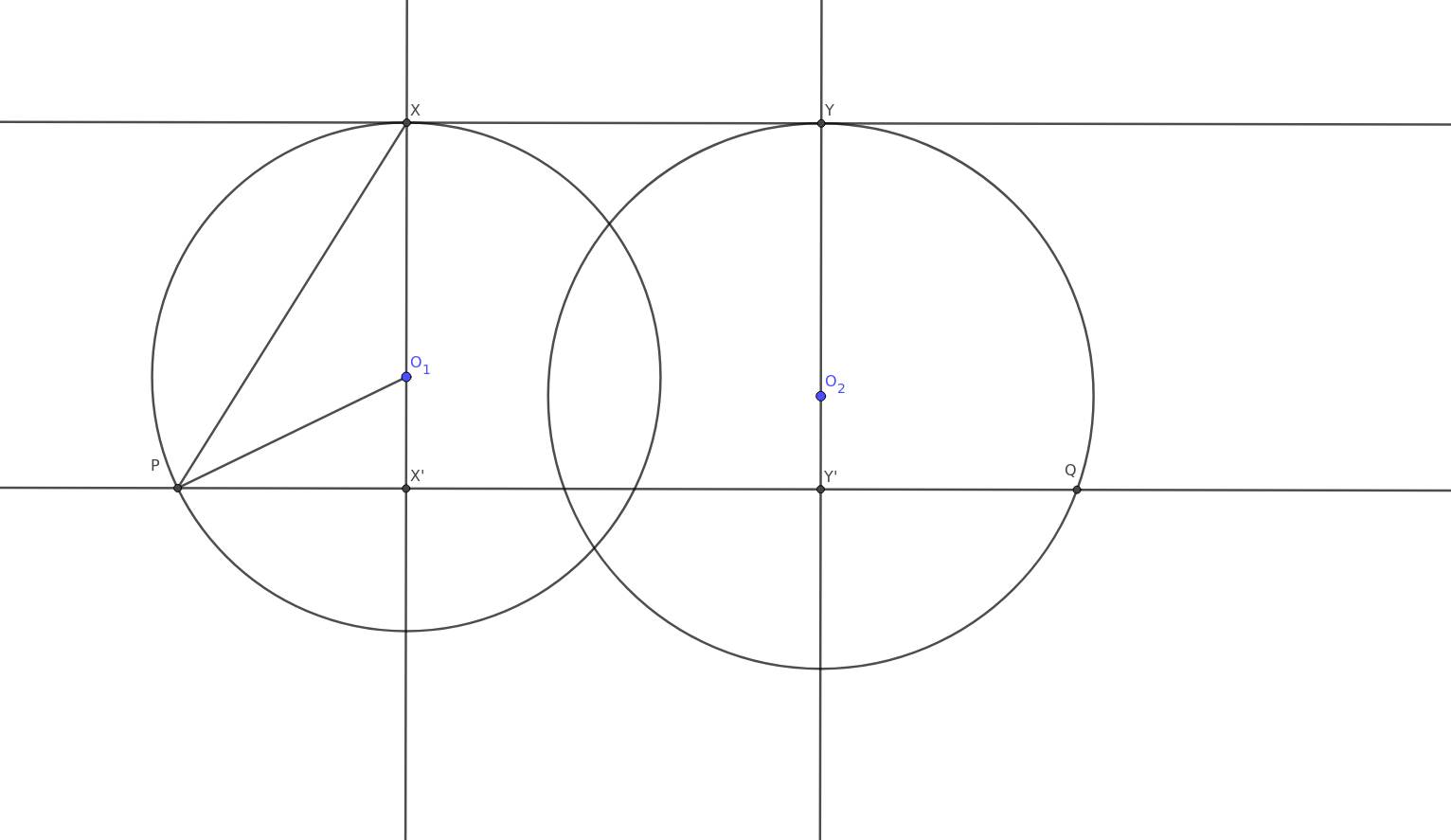
Kuvassa on ratkaisua varten muutama ylimääräinen piste. Tämä tehtävä on hyvä sinilauseen soveltamiselle monestakin syystä. Ensimmäinen syy on hyvän tuntomerkin löytyminen, tulee osoittaa, jonkin lausekkeen ($\frac{XP}{YQ}$) olevan vakio. Toinen hyvä piirre on kuvion yksinkertaisuus, tehtävässä ei esiinny toistakymmentä vaikeasti lähestyttävää pistettä. Näistä syistä sinilause on hyvinkin varteenotettava vaihtoehto.

Nimetään ensiksi muutama laskemista helpottava asia: Olkoot $O_1$ ja $O_2$ ympyröiden keskipisteet, $X’$ ja $Y’$ pisteiden $X$ ja $Y$ projektiot suoralle $m$, ympyröiden säteet $r_1$ ja $r_2$, ja $XX’ = YY’ = d$ suorien $l$ ja $m$ välinen etäisyys. Olkoot vielä $\angle O_1PX’ = \alpha$ ja $\angle O_2QY’ = \beta$. Suunnitelmana on ilmoittaa pituudet $XP$ ja $YQ$ lukujen $d$, $r_1$ ja $r_2$ avulla, ja toivoa, että lopussa $d$ supistuu pois (näin tapahtuu, sillä muuten tehtävänannon väite ei pätisi). Tämä on ainakin teoriassa mahdollista, sillä muuttujat $d$, $r_1$ ja $r_2$ yksikäsitteisesti määrittävät konfiguraation. Hyökkäämme suoraan janojen $XP$ ja $YQ$ kimppuun, ja koitamme edetä siitä.

Helpoin tapa saada $XP$ selville lienee kolmiosta $XX’P$. Käytetään sinilauseen erikoistapausta suorakulmaiselle kolmiolle. Saamme

$$XP = \frac{XX'}{\sin(\angle XPX')} = \frac{d}{\sin(\angle XPX')}$$

Intuitio kertoo, että $\angle XPX’$ on suoraan esitettävissä kulman $\alpha$ avulla, ja näin onkin:

$$\angle XPX' = 90^{\circ} - \angle PXX' = 90^{\circ} - \frac{\angle PO_1X'}{2} = 90^{\circ} - \frac{90^{\circ} - \alpha}{2} = \frac{\alpha}{2} + 45^{\circ}$$

Siispä

$$XP = \frac{d}{\sin(\frac{\alpha}{2} + 45^{\circ})}$$

Saamme vastaavasti

$$YQ= \frac{d}{\sin(\frac{\beta}{2} + 45^{\circ})}$$

Nyt,

$$\frac{XP}{YQ} = \frac{\sin(\frac{\beta}{2} + 45^{\circ})}{\sin(\frac{\alpha}{2} + 45^{\circ})}$$

Lausekkeet saattavat näyttää hieman pahalta, ja kisatilanteessa kannattaakin tässä kohtaa varmistaa suunnitelman toimivuus. Voimme kirjoittaa trigonometrisen lausekkeemme kohtalaisen vaivan jälkeen pelkästään muuttujien $\sin(\alpha)$ ja $\sin(\beta)$ avulla, ja tiedämme, että

$$\sin(\alpha) = \frac{O_1X'}{r_1} = \frac{d - r_1}{r_1}$$

(olettaen $d > r_1$, $d \leq r_1$ on analoginen), eli se on hallinnassa. Suunnitelma vaikuttaa siis pitävältä, eli voidaan vain puskea eteenpäin. Jos usko meinaa loppua, kannattaa muistella mietelausetta “sinilause tappaa kaiken”.

Käytämme ensiksi sinin summakaavoja jakaaksemme lausekkeemme pienempiin palasiin.

$$\frac{\sin(\frac{\beta}{2} + 45^{\circ})}{\sin(\frac{\alpha}{2} + 45^{\circ}} = \frac{\sin(\frac{\beta}{2})\cos(45^{\circ}) + \cos(\frac{\beta}{2})\sin(45^{\circ})}{\sin(\frac{\alpha}{2})\cos(45^{\circ}) + \cos(\frac{\alpha}{2})\sin(45^{\circ})}$$

Sillä $\sin(45^{\circ}) = \cos(45^{\circ})$, voidaan nämä supistaa pois, jolloin jäljelle jää vain

$$\frac{\sin(\frac{\beta}{2}) + \cos(\frac{\beta}{2})}{\sin(\frac{\alpha}{2}) + \cos(\frac{\alpha}{2})}$$

Nyt tulee ongelma eteen: miten saadaan ilmoitettua $\sin(\frac{x}{2})$ muuttujan $\sin(x)$ avulla? Kokemus kertoo, että tämä voidaan ratkaista:

Lemma

Puolikkaan sinin kaava:

$$\sin(\frac{x}{2}) = \sqrt{\frac{1-\cos(x)}{2}}$$

Puolikkaan kosinin kaava:

$$\cos(\frac{x}{2}) = \sqrt{\frac{\cos(x) + 1}{2}}$$

Huomaa, että yleisessä tapauksessa tulisi plus-miinus-merkkejä, mutta meidän tilanteessamme nämä eivät ole tärkeitä.

Lemman todistus

Sijoitetaan todistettaviin lausekkeisiin yksinkertaisuuden vuoksi $y = \frac{x}{2}$. Sinin tapauksessa tulee osoittaa, että $\sin(y)^2 = \frac{1 - \cos(2y)}{2}$. Tämän osoittaminen todeksi on suoraviivaista: kaksinkertaisen kosinin kaavalla ja identiteetillä $\cos^2(y) = 1 - \sin^2(y)$ saadaan $\cos(2y) = \cos^2(y) - \sin^2(y) = 1 - 2\sin^2(y)$. Sijoittamalla tämän todistettavaan yhtälöön saamme $0 = 0$. Vastaavasti osoitetaan puolikkaan kulman kosinin kaava.

Ratkaisun viimeistely

Näitä kaavoja soveltamalla lausekkeemme muuttuu muotoon

$$\frac{ \sqrt{\frac{\cos(\beta) + 1}{2}} + \sqrt{\frac{1 - \cos(\beta)}{2}}}{ \sqrt{\frac{\cos(\alpha) + 1}{2}} + \sqrt{\frac{1 - \cos(\alpha)}{2}} } = \frac{ \sqrt{\cos(\beta) + 1} + \sqrt{1 - \cos(\beta)}}{ \sqrt{\cos(\alpha) + 1} + \sqrt{1 - \cos(\alpha)}}$$

Vielä on yksi haaste selätettävänä: miten voimme osoittaa tämän olevan vakio? Tiedämme mitä ovat sinit kulmista $\alpha$ ja $\beta$, mutta kosineille meillä ei ole mukavaa esitystä. Onneksemme juurilausekkeista pääsee eroon seuraavalla tempulla: haluamme osoittaa yllä olevan lausekkeen olevan vakio. Sillä se on positiivinen, riittää osoittaa sen neliön olevan vakio. Näin pääsemme näppärästi eroon juurilausekkeista, ja kaiken lisäksi saamme kosinit muutettua sineiksi, nimittäin:

$$\frac{ {\Big( \sqrt{\cos(\beta) + 1} + \sqrt{1 - \cos(\beta)} \Big)}^2}{ \Big( \sqrt{\cos(\alpha) + 1} + \sqrt{1 - \cos(\alpha)} \Big)^2 } = \frac{2 + 2\sqrt{1-\cos^2(\beta)}}{2 + 2\sqrt{1-\cos^2(\alpha)}} = \frac{1 + \sin(\beta)}{1 + \sin(\alpha)}$$

Nyt tuntuu sopivalta hetkeltä sijoittaa

$$\sin(\beta) = \frac{d - r_2}{r_2}, \ \ \ \sin(\alpha) = \frac{d - r_1}{r_1}.$$

Loppu onkin hyvin helppo: $\frac{1 + \frac{d - r_2}{r_2}}{1 + \frac{d - r_1}{r_1}} = \frac{\frac{d}{r_2}}{\frac{d}{r_1}} = \frac{r_1}{r_2}.$ Tämä on selvästi $d$:stä riippumaton vakio. Olemme valmiit. Kaiken lisäksi tiedämme, että $\frac{XP}{YQ}$ on tämän neliöjuuri.

Kommentti

Mitä tästä voidaan oppia? Ensinnäkin, kuvioon kannattaa merkitä joitakin laskemista helpottavia janoja, tässä tapauksessa mm. $XX’$ ja $PO_1$. Suunnitelma tässä tehtävässä oli suoraviivainen: ilmoitetaan haluamamme suure jollain helpommilla muuttujilla, joita tässä tapauksessa olivat $\sin(\alpha)$ ja $\sin(\beta)$, ja lopulta kirjoitetaan nämä tehtävän vakioiden avulla. Ainoastaan toteutus oli hieman työläs, mutta loppukädessä se ei ollut kovin vaikea. Ratkaisussa vain kirjoitettiin lauseke, jonka piti olla vakio, ja sovellettiin tunnettuja trigonometrisia identiteettejä lausekkeen sieventämiseksi.

Me tietyllä tavalla tiedämme, että ratkaisumme toimii jos vain laskemme ja sieventelemme tarpeeksi, vaikkakin laskemista voi joskus tulla varsin paljon. Lopussa näemme heti, jos jotain meni pieleen (vastaus ei olekaan vakio). Silloin voimme kulkea taaksepäin etsimään virheitä, ja korjaamalla ne olemme valmiit.

Pari asiaa, jotka henkilökohtaisesti olen huomannut tärkeiksi sinilauseratkaisua suunnitellessa:

Onko meillä tarpeaksi tietoa tehtävän kulmista? Jos kulmien suuruuksia on vaikea yhdistää toisiinsa, vaikka ne riippuvat toisiinsa, voi ratkaiseminen mennä vaikeaksi. Tutkitaan esimerkiksi tehtävää, jossa esiintyy kolmio ja sen mediaanit. Mediaanin ja kolmion sivun välinen kulma on vaikea laskea, mikä on varoittava tuntomerkki. Toisaalta, tässä tapauksessa on hyvin tietoa janojen pituuksien suhteista, sillä mediaani puolittaa vastakkaisen sivun, ja jakavat toisensa suhteessa $2:1$. On tehtäväkohtaista kumpi ominaisuus painaa enemmän.

Millainen todistettava väite on? Jos pyrimme osoittamaan, että kolme suoraa leikkaavat samassa pisteessä, ei sinilause välttämättä ole paras lähestymistapa. Toisaalta, jos esimerkiksi haluamme todistaa väitteen muotoa “$\frac{AB}{CD}$ on vakio”, sinilause ei ole hullumpi idea.

Huomattakoon vielä, että sinilauseella ei aina tarvitse hyökätä koko tehtävän kimppuun, vaan sillä voidaan todistaa myös oleellisia lemmoja. Esimerkiksi harjoitustehtävänä on vuoden 2016 IMOn tehtävä 1, jonka väite on nimenomaan yllä pelätty kolmen suoran leikkaaminen samassa pisteessä, mutta tehtävään löytyy sinilausetta apuna käyttävä ratkaisu.

Harjoitustehtäviä

Tässä on vain pari tehtävää sinilausebashin harjoittelemiseksi, mutta harjoittelua varten sopii hyvinkin suuri osa kilpailuissa esiintyvistä geometrian tehtävistä.

MAOLin loppukilpailu 2018, T3. (Perhoslause)

Olkoon ympyrällä $\omega$ jänteet $AB$ ja $CD$, jotka leikkaavat pisteessä $M$. Olkoon $PQ$ se jänne, jonka keskipiste on $M$. Janat $AC$ ja $PQ$ leikkaavat pisteessä $X$, ja janat $BD$ ja $PQ$ leikkaavat pisteessä $Y$. Osoita, että $MX = MY$.

IMO 2016 T1

Kolmiolla $BCF$ on suora kulma kärjessä $B$. Olkoon $A$ piste suoralla $CF$ siten, että $FA = FB$ ja piste $F$ sijaitsee pisteiden $A$ ja $C$ välissä. Valitaan piste $D$ siten, että $DA = DC$ ja $AC$ puolittaa kulman $\angle DAB$. Valitaan piste $E$ siten, että $EA = ED$ ja $AD$ puolittaa kulman $\angle EAC$. Olkoon $M$ janan $CF$ keskipiste. Olkoon $X$ se piste, jolla $AMXE$ on suunnikas (missä $AM \parallel EX$ ja $AE \parallel MX$). Osoita, että suorat $BD$, $FX$ ja $ME$ kulkevat saman pisteen kautta.