Catalanin lukujen yleistys
Tässä postauksessa käydään läpi eräs Suomen loppukilpailutehtävä, joka osoittautuu Catalanin lukujen yleistykseksi.
MAOL:n loppukilpailu 2014, Tehtävä 3
Pisteet $P = (a, b)$ ja $Q = (c, d)$ ovat $xy$-tason ensimmäisessä neljänneksessä, ja $a, b, c$ sekä $d$ ovat kokonaislukuja, joille $a<b, a<c, b<d$ ja $c<d$. Reitti pisteestä $P$ pisteeseen $Q$ on positiivisten koordinaattiakselien suuntaisista, yksikön pituisista askelista muodostuva murtoviiva, ja sallittu reitti on reitti, joka ei leikkaa eikä kosketa suoraa $x = y$. Montako sallittua reittiä on?
Tehtävänannon ymmärtämisen jälkeen kannattaa ensin miettiä tehtävään ratkaisua. Ensin kannattaa yrittää määrittää kaikkien reittien määrä. Myös oikean vastauksen arvaileminen on hyvä tapa lähestyä tehtävää, vaikka ei todistusta keksisikään.
Ratkaisu 1 (malliratkaisu)
Tämän ratkaisun ymmärtämistä auttaa ja tehtävän mielenkiintoisuutta lisää, jos tuntee Catalanin luvut, koska osoittautuu, että tehtävän asetelma on oikeastaan niiden yleistys.
Asetelmaa kannattaa ajatella suorakulmiona, jonka vasemmasta alakulmasta tulee päästä oikeaan yläkulmaan siten, että oikeasta alakulmasta on lohkaistu pois alue, jolle ei saa mennä. Unohdetaan nyt pois lohkaistu alue hetkeksi. Yhteensä askelia matkalla kulmasta kulmaan on $n=(c-a)+(d-b)$ kappaletta. Näistä $k=(d-b)$ on ylöspäin. Voimme ottaa nämä askeleet ylöspäin milloin vain haluamme, joten mahdollisia reittejä on nyt
kappaletta.
Asetelmaa tarkastelemalla huomataan, että tämä vastaus on oikea vastaus myös koko tehtävään, jos $c<b$. Oletetaan sitten, että $b \le c$.
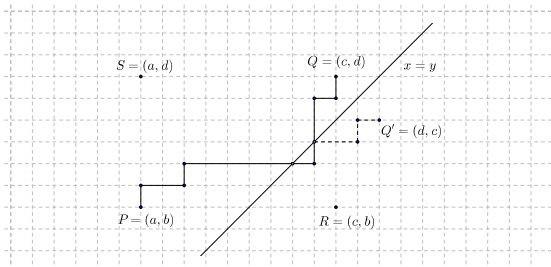
Kuvassa näkyy tehtävän asetelma. Lähde: malliratkaisu (MAOL)
Tulee vähentää kaikista reiteistä kielletyt reitit. Yritetään laskea niiden määrä. Jokaisella kielletyllä reitillä on vähintään yksi kohta, jossa se leikkaa suoran $x=y$. Tarkastellaan viimeistä tällaista leikkauspistettä, olkoon vaikka $T$. Olkoon pisteen $Q$ peilaus suoran $x=y$ suhteen $Q’$ Selvästi reittejä $T$:stä $Q$:hun on yhtä paljon kuin reittejä $T$:stä $Q’$:uun. Otetaan nyt tarkasteluun kaikki mahdolliset kielletyt reitit $P$:stä $Q$:hun. Peilataan jokaisen reitin pisteen T jälkeinen osuus suoran $x=y$ suhteen, eli muutetaan ylöspäin etenemiset vaakaan etenemisiksi ja päinvastoin. Kiellettyjen reittien määrä ei muutu, mutta nyt jokainen kielletty reitti päätyy pisteen $Q$ sijaan pisteeseen $Q’$. Lisäksi kaikki pisteestä $P$ pisteeseen $Q’$ menevät reitit leikkaavat suoraa $x=y$. Siis kiellettyjen reittien määrä on sama kuin pisteestä $P$ pisteeseen $Q’$ menevien reittien määrä.
Koska $Q’$ on $Q$:n peilaus suoran $x=y$ suhteen, pätee $Q’=(d, c)$. Aiempaa vastaavalla päättelyllä kiellettyjä reittejä eli reittejä $P$:stä $Q’$:uun on yhteensä ${d-a+c-b \choose c-b}$. Tämä tarkoittaa, että sallittuja reittejä on yhteensä
Catalanin luvut
Edellä on riittävä ratkaisu kilpailutehtävään, mutta ajatellaanpa seuraavaksi tehtävän erikoistapausta, jossa $b=a+1$ ja $d=c+1$, ja lisäksi vielä $c>a$. Oikea vastaus tähän on siis Tällaisessa lähtötilanteessa olemme yhden askeleen suoraa $x=y$ ylempänä, ja jokaisella askeleella voimme päättää, lähdemmekö kauemmas tästä suorasta, vai menemmekö lähemmäs sitä. Lopputilanteessa meidän tulee olla yhden askeleen päässä suorasta, mutta emme saa missään vaiheessa törmätä siihen. Tämä asetelma on täsmälleen sellainen, jossa $n:$s Catalanin luku kertoo, kuinka monta $2n:$ n mittaista sallittua reittiä on. Tässä tapauksessa $2n=(c+d)-(a+b)=2d-2b$, joten $n:$s Catalanin luku on
Tässä erikoistapauksessa saamme siis vastauksen myös Catalanin lukujen avulla. Peilausratkaisu antaa kuitenkin vastauksen kaikkiin mahdollisiin tehtävänannon mukaisiin tapauksiin. Tehtävänannon asetelma on siis Catalanin lukujen yleistys.
Huomatutus
Catalan-postauksessa oleva bittijonoratkaisu äskeistä erikoistapausta vastaavaan kombinatoriseen ongelmaan on oikeastaan formaalisti muotoiltu peilaus, eli käyttää samaa ideaa kuin tämän kilpatehtävän ratkaisu.
Ratkaisu 2 (induktio)
Ratkaisussa 1 ei ole mitään vikaa, mutta se voi olla vaikea keksiä. Olli Järviniemi päätyikin toisenlaiseen ratkaisuun, joka on hieman pidempi, mutta käyttää menetelmänään (monivaiheista) induktiota, joka tehtäviä tehdessä on varmaankin peilausta helpommin mieleen tuleva idea.
Induktion ideana on käyttää hyväksi sitä faktaa, että ongelman erikoistapaus, missä $d - c = 1$ ja $b - a = 1$ on ratkaistu Catalanin lukujen muodossa. Tätä kautta voimme edetä induktion kautta eteenpäin käyttäen jo ennestään ratkaistuja tapauksia.
Osoitetaan induktiolla muuttujan $d-c$ suhteen, ($a$ ja $b$ voivat olla mielivaltaisia, kunhan ne toteuttavat tehtävänannon ehdot) että sallittujen reittien määrä on
kun $b\le c$, ja
kun $c<b$
Osoitetaan ensin pohjatapaus $d-c=1$. Tämä tarkoittaa siis sitä, että jälkimmäinen piste on yhden askeleen päässä suorasta $x=y$.
Osoitetaan pohjatapaus induktiolla muuttujan $d-b$ suhteen. Tämä muuttuja kuvaa siis sitä, kuinka paljon mennään ylöspäin. Kun $d-b=0$, niin sallittuja reittejä on selvästi vain yksi, kuten kuuluukin. (Alkuperäisen tehtävänannon ehtojen mukaan $d>b$, mutta ei nyt välitetä siitä.) Oletetaan sitten, että väite pätee, kun $d-b=k$ ja osoitetaan, että se pätee, kun $d-b=k+1.$
Osoitetaan tämä induktiolla muuttujan $a$ suhteen siten, että $a$ kulkee arvosta $b-1$ negatiiviseen suuntaan. Tässä induktiossa pohjatapaus on $b=a+1$ ja $d=c+1$, eli Catalanin lukujen nojalla alkuperäinen väitteemme pätee. Oletetaan sitten, että väitteemme pätee, kun $a=b-m$ ja osoitetaan, että se pätee, kun $a=b-m-1$.
Tiedämme, että reittien määrä pisteestä $(d-k-m-1, d-k)$ pisteeseen $(d-1,d)$ toteuttaa väitteemme. Tämä seuraa induktio-oletuksesta liittyen induktioon muuttujan $d - b$ suhteen. Myös reittien määrä pisteestä $(d-k-m, d-k-1)$ pisteeseen $(d-1, d)$ on kaavan ilmoittama, mikä seuraa induktiosta muuttujan $a$ suhteen.
Nyt reittien määrälle $S$ pisteestä $ (d-k-m-1, d-k-1) $ pisteeseen $(d-1, d)$ pätee:
Tämä johtuu siitä, että pisteestä $(d - k - m - 1, d - k - 1)$ reittien määrä pisteeseen $(d - 1)$ menee ensimmäisellä askeleella joko ylös tai oikealle.
Pascalin identiteetin nojalla lauseke on sama kuin
Tämä todistaakin indukioaskeleen ja siten koko pohjatapauksen $d-c=1$.
Oletetaan sitten, että väitteemme pätee, kun $d-c=k$ ja osoitetaan väite, kun $d-c=k+1$. Osoitetaan tämä väite induktiolla muuttujan $c-a$ suhteen. Kun $c-a=0$ (Näinkään ei saisi olla, mutta ei välitetä tästäkään), reittejä on selvästi $1$, kuten väitteemme mukaan pitikin olla. Oletetaan, että väitteemme pätee, kun $c-a=m$, ja osoitetaan se, kun $c-a=m+1$. Saamme induktioaskeleen otettua Pascalin identiteetin nojalla täysin vastaavasti kuin tapauksen $d-c=1$ induktiossa.
Nyt siis olemme osoittaneet, että kaikilla tehtävänannon mukaisilla luvuilla väitteemme, eli vastaus tehtävään, pätee. Olemme siis valmiit. Vastaus tehtävään on
kun $b\le c$, ja
kun $c<b$.