MAOLin loppukilpailu 2019
Tässä postauksessa esitetään vuoden 2019 MAOLin loppukilpailun tehtäviin ratkaisuhahmotelmat sekä kilpailutilannetta kisaajan näkökulmasta.
Ensiksi tehtävät:
Tehtävät
Tehtävä 1
Ratkaise, mille luvuille $x$ on voimassa
kun $0 < x \le 1$.
Tehtävä 2
Kun $x$ on reaaliluku, tarkoittaa $\lfloor x \rfloor$ suurinta kokonaislukua $n$, jolle $n \le x$. Esimerkiksi $\lfloor 4,2 \rfloor = 4$, $\lfloor \pi \rfloor = 3$ ja $\lfloor 8 \rfloor = 8$. Todista, että luku $\lfloor (2 + \sqrt{5})^{2019} \rfloor$ ei ole alkuluku.
Tehtävä 3
Olkoon $ABCD$ ympyrän jännenelikulmio, jonka sivu $AB$ on samalla ympyrän halkaisija. [Jännenelikulmio tarkoittaa nelikulmiota, jonka kärjet sijaitsevat ympyrän kevällä.] Janat $AC$ ja $BD$ leikkaavat pisteessä $E$ ja janojen $AD$ ja $BC$ jatkeet pisteessä $F$. Jana $EF$ leikkaa ympyrää pisteessä $G$ ja janan $EF$ jatke leikkaa halkaisijan $AB$ pisteessä $H$. Ooista, että jos $G$ on janan $FH$ keskipiste, niin $E$ on janan $GH$ keskipiste.
Tehtävä 4
Määritellään lukujono asettamalla
kun $n$ on positiivinen kokonaisluku. Määritä kaikki ne positiiviset kokonaislukumodulot $m$, joissa tämä lukujono on lopulta jaksollinen, ts. on olemassa sellaiset positiiviset kokonaisluvut $K$ ja $s$, että $a_n \equiv a_{k + s} \pmod{m}$. kun $k \ge K$ on kokonaisluku.
Tehtävä 5
Opettajalla tiedetään olevan $2^k$ omenaa jollakin $k \in \mathbb{N}$. Hän syö oppilaiden nähden yhden omenoista itse ja jakaa loput oppilailleen $A$ ja $B$ niin, ettei kumpikaan näe, kuinka monta toinen saa. $A$ ja $B$ eivät tunne lukua $k$. He ovat kuitenkin ennalta valinneet huomaamattoman tavan paljastaa yhdellä ainoalla merkillä toisilleen jotakin omenoiden määrästä: Kumpikin raapii päätään oikealla, avsemmalla tai molemmilla käsillään saamiensa omenoiden lukumäärän mukaan. Opettajan ällistykseksi oppilaat tietävätkin aina, kumpi sai omenoita enemmän tai että opettaja söi ainoan omenan itse. Miten tämä on mahdollista?
Yleisiä kommentteja
Kilpailu oli vaikea. Voitto irtosi 17 pisteellä, toinen sija 16 pisteellä, ja jaetut sijat kolme ja neljä 14 pisteellä kunkin tehtävän ollessa kuuden pisteen arvoinen. Mielestäni mikään tehtävistä ei ollut ylitsepääsemättömän vaikea, mutta toisaalta mikään tehtävä ei ollut aivan triviaali. Tämä näkyy tuloksissa: kullekin tehtävälle 2-5 löytyi joku, joka oli saanut tehtävän täysillä pisteillä ratkaistua, mutta toisaalta mistään tehtävästä ei tullut keskimäärin kovin suuria pisteitä. Tulostaulukko löytyy MAOLin sivuilta tästä tiedostosta.
Oma kilpailukokemus
En jännittänyt kisaa kovin paljoa ennen kilpailua, ja olin melko itsevarma: valmennuskoe viikkoa ennen loppukilpailua pidetyssä valmennusviikonlopussa oli sujunut hyvin. En kuitenkaan pitänyt voittoa itsestäänselvyytenä, mutta pidin itseäni yhtenä ennakkosuosikeista.
Kilpailun alettua katselen tehtäväpaperia. Olen hieman yllättynyt: mikään tehtävistä ei vaikuttanut triviaalilta. Vanhoissa kilpailutehtävissä oli usein ollut vähintään yksi tehtävä, josta harjoitellessani olin nähnyt suoraan ratkaisuun johtavan idean. En vielä tässä kohtaa ole varma siitä, onko kyseinen tehtäväsetti tavallista vaikeampi.
Ollessani vielä kokemattomampi kilpailija mietin miltei aina kilpailun alkaessa tehtävien olevan tavallista vaikeampia. Tämä varmaankin johtuu siitä, että ratkaisut ovat helppoja, kun ne tietää - siis vanhat kisatehtävät tuntuvat hyvin helpoilta, koska niiden ratkaisut tietää jo. Kokemuksen kautta olen osannut pienentää tämän ajatuksen vaikutusta, mutta nyt MAOLin loppukilpailussa tunne iski jälleen. Osasyynä tähän on tietysti se, että tehtävät todella olivat vaikeampia kuin yleensä.
Koitqn nopeasti ratkaista tehtävän 1. Ajattelen, että siihen on jokin lyhyt ja elegantti ratkaisu, onhan kyseessä kokeen ensimmäinen tehtävä. Kokeilen trigonometrisia sijoituksia, mutten saa mitään alkuperäistä epäyhtälöä sievempää. Muutaman minuutin jälkeen siirryn tehtävään 2.
Tehtävä 2 on minulle käytännössä jo tuttu, olinhan edellisessä blogipostauksessani kirjoittanut hyvin samankaltaiseen tehtävään ratkaisun. Kirjoitan tehtävään nopeasti ratkaisun (kts. ratkaisut alla), mutta teen kahden pisteen arvoisen huolimattomuusvirheen. Noin 20-30 minuuttia kilpailun alusta minulla on ratkaisu paperilla.
Tämän jälkeen pompin nopeasti tehtävästä toiseen (“Pakkohan täällä jossain on jokin helppo tehtävä olla!”). Lukuteoria on vahvuuteni ja lempiosa-alueeni kilpailumatematiikasta, joten yritän ratkaista tehtävän 4, minkä jälkeen pääsisin keskittymään muihin tehtäviin. Onnistun tässä ilman suurempia ongelmia, ja tunti kilpailun alusta minulla on kaksi tehtävää ratkaistuna.
En osaa sanoa tarkasti, mihin loput kaksi tuntia tarkalleen meni. Koitin melko tasavertaisesti tehtäviä 1, 3, 5. Loppua kohden sain aika hyvää edistystä tehtävään 3. Tunsin olevani kaukana kokonaisesta ratkaisusta kilpailun loputtua - olisin arvioinut ratkaisua kahden pisteen arvoiseksi, optimistisesti kolmen pisteen ratkaisuksi. Yllätyinkin kovasti saadessani palkintojenjaon jälkeen tietää saaneeni 5/6 pistettä.
Kilpailun loputtua en juurikaan puhunut muille omasta suorituksestani, koska halusin säilyttää jännitystä palkintojenjakoon asti. Illalla hotellilla olin kuitenkin melkein varma, etten voittaisi kilpailua.
Palkintojenjakopäivänä keskutelimme edellisen päivän hiljasuudesta poiketen avoimesti omista suorituksistamme. Päädyimme siihen johtopäätökseen, että Roope Salmi voittaisi kilpailun (vaikkei Roope edes ollut paikalla tuloksista puhuttaessa!). Meillä oli paljon vapaa-aikaa, jonka käytimme pääosin pöytäjalkapallon pelaamiseen.
Palkintojenjaossa minulle selvisi, että olin voittanut kilpailun. Olin helpottunut.
Ratkaisuhahmotelmat
Tehtävä 1
Kirjoitetaan epäyhtälö muodossa
Neliöidään yhtälö puolittain, jolloin tehtävä palautuu kolmannen asteen epäyhtälön ratkaisemiseksi. Tällä kolmannen asteen polynomilla on rationaalinen juuri $\frac{3}{5}$, joka voidaan löytää tunnetulla lauseella. Epäyhtälö pätee siis niillä $x$, joilla $x \ge \frac{3}{5}$. Yksityiskohtiin ei mennä tässä.
Huomautus
Ratkaisu on kieltämättä helppo, vaikkakin hieman pitää laskea. Minulla (ja ilmeisesti monilla muilla) ongelmaksi tuli se, että ajattelin tähän olevan jotain eleganttia. Kukaan ei tästä tehtävästä saanut kolmea pistettä enempää!
Trigonometristen sijoitusten kautta voisi löytyä ratkaisu, vaikken olekaan sellaista löytänyt. $\frac{3}{5}$ on siitä pyöreä luku, että $\cos(\alpha) = \frac{3}{5} \implies \sin(\alpha) = \frac{4}{5}$, mikä myös vihjaa trigonometrisen ratkaisun olemssaolosta.
Kilpailun aikana olin (virheellisesti) palauttanut tehtävän kolmannen asteen epäyhtälöksi, mutten luottanut ratkaisumenetelmään tarpeeksi. Lopputuloksena yksi piste.
Tehtävä 2
Ratkaisumenetelmä on hyvin samanlainen kuin tässä blogipostauksessa. Yksityiskohtiin ei tämän vuoksi juututa kovin tarkasti.
Valitaan $a_0 = 2$, $a_1 = 4$ ja
Tällöin $a_n = (2 + \sqrt{5})^n + (2 - \sqrt{5})^n$. Siispä $a_n = \lfloor (2 + \sqrt{5})^n \rfloor$ kaikilla parittomilla $n$. Haluttu luku $a_{2019}$ on rekursioyhtälön nojalla parillinen (helpolla induktiolla $2 \mid a_n$ kaikilla $n$), mikä todistaa väitteen.
Huomautus
Kilpailussa tein pienen ajatusvirheen $2 - \sqrt{5} > 0$. Tämän seurauksena päädyin tutkimaan lukujonoa $b_n = a_n - 1$, ajatellen halutun luvun olevan $b_{2019}$. Ratkaisin tämän ongelman osoittamalla $b_{2019} \equiv 0 \pmod{3}$. Lopputulos neljä pistettä, mikä on mielestäni reilua.
Tehtävä 3
Akseli Jussinmäki kertoi minulle seuraavan ratkaisun, jonka kertoi kuulleensa toiselta kilpailijalta. Tulostaulukon perusteella ratkaisu on varmaankin Asla Heiskasen, mutten ole tästä aivan varma.
Kuva tehtävästä:
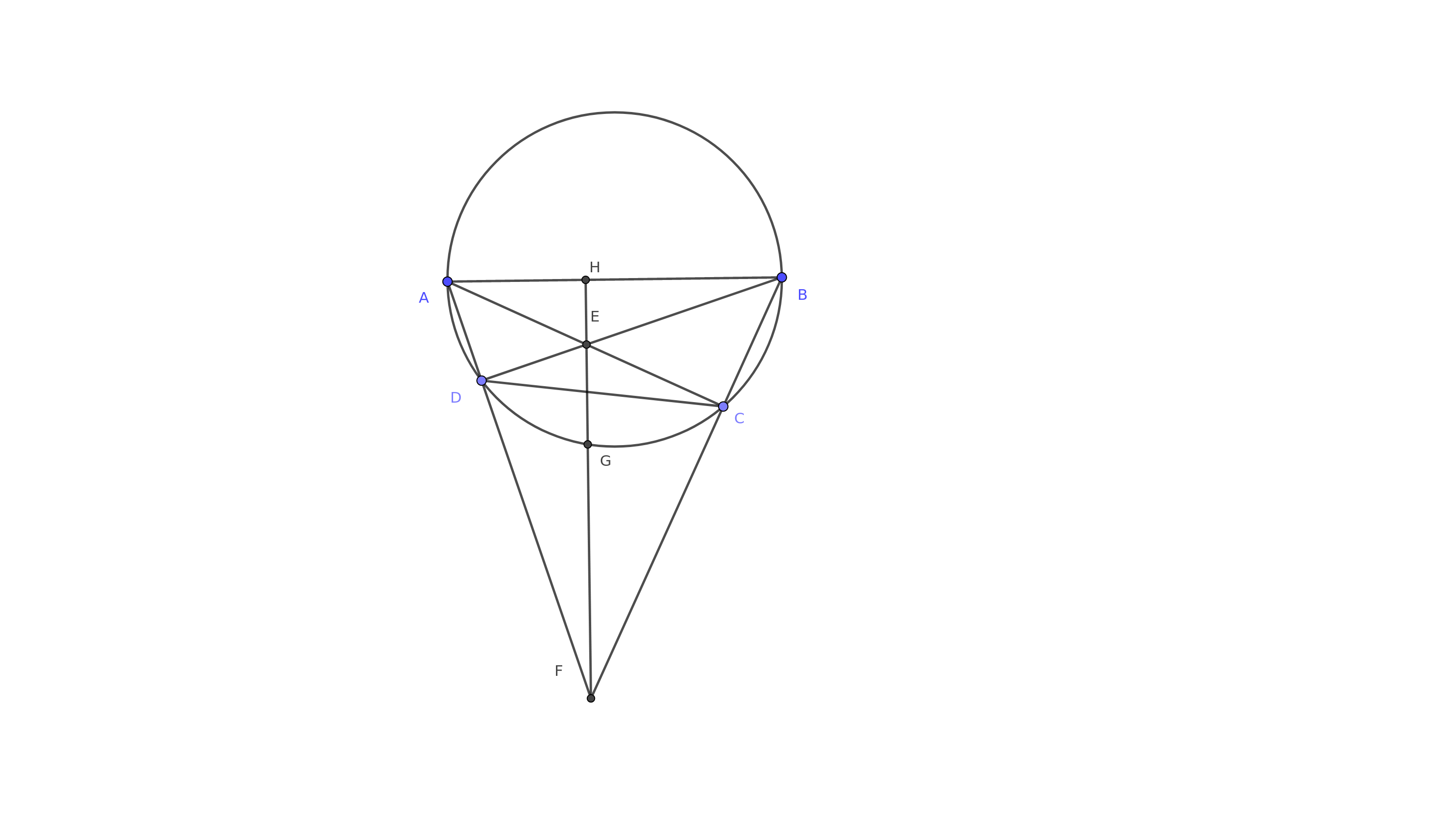
Lemma 1
$FH \perp AB$.
Todistus
$AC \perp BF$ ja $AF \perp BD$. Siis $E$ on kolmion $ABF$ kahden korkeusjanan leikkauspiste, eli myös kolmas korkeusjana kulkee $E$:n kautta. Siispä $HF$ on kolmion $ABF$ korkeusjana, mikä todistaa väitteen.
Lemma 2
$AHCF$ on jännenelikulmio.
Todistus
Lemman 1 nojalla $\angle AHF = \angle ACF = 90^{\circ}$, mikä todistaa väitteen.
Peilataan piste $G$ halkaisijan $AB$ suhteen pisteelle $G’$ (ei näy kuvassa), jolloin myös $G’$ on kuvan ympyrän kehällä, ja lisäksi $G’H = HG$.
Ideana on soveltaa pisteen potenssia kahdesti. Käytetään ensin pisteen potenssia pisteelle $E$ lemman 2 mukaisen jännenelikulmion $AHCF$ suhteen. Saamme
Toisaalta soveltamalla pisteen $E$ potenssia jännenelikulmion $AG’CG$ ympärysympyrälle saadaan
Siispä
Väite seuraa tästä: olkoon $a = FG = GH = HG’$ ja $x = EH$. Yhtälö on ekvivalenttia yhtälön
kanssa. Tämä muuttuu muotoon $a = 2x$, eli $EH = x = a - x = EG$, mikä oli todistettavana.
Huomautus
Kokeilin monia erilaisia lähestymistapoja tehtävään, mutta mikään ei tuntunut toimivan. Totesin kyllä lemmat 1 ja 2, mutta tässä kohtaa ratkaisuni ajautui eri suuntaan kuin yllä esitetty. Lopputuloksena viisi pistettä.
Tehtävä 4
Vastaus: kaikki $m$ toimii.
Lemma 1
Olkoot $m_1$ ja $m_2$ yhteistekijättömiä. Lukujono $a_n$ on jostain pisteestä jaksollinen modulo $m_1m_2$ jos ja vain jos $a_n$ on jaksollinen jostain pisteestä lähtien moduloissa $m_1$ ja $m_2$.
Todistus
Jätetään harjoitustehtäväksi. Vastaava idea (redusoidaan väite alkulukujen potensseihin) esiintyy usein lukuteoriassa, minkä vuoksi suosittelen lemman todistamista itse.
Lemma 2
$a_n$ on jaollinen modulo $p^k$ kaikilla alkuluvuilla $p$ ja kaikilla $k \in \mathbb{Z_+}$.
Todistus
Olkoon $s$ lukujen $\phi(p^k)$ ja $p^k$ pienin yhteinen jaettava. Osoitetaan, että tämä kelpaa jaksoksi. Tutkitaan kolmea tapausta:
- $p$ ei jaa lukuja $n, n-1$. Tällöin
Käytetään Eulerin lausetta, kantalukuina luvun $p^k$ kanssa yhteistekijättömät luvut $n$ ja $n-1$. Saadaan $n^{n+s} \equiv n^n \pmod{p^k}$, ja vastaavasti $(n-1)^{n+s+1} \equiv (n-1)^{n+1} \pmod{p^k}$. Siis
Siis yhtälö $a_{n+s} \equiv a_n \pmod{p^k}$ pätee kaikilla $n$, joilla $p \nmid n(n-1)$.
- $p$ jakaa luvun $n$. Tutkitaan nyt vain niitä $n$, joilla $n \ge k$. Tällöin $n^n \equiv 0 \pmod{p^k}$. Siispä
Jälleen Eulerin lausetta soveltamalla (huomaa, että $syt(p^k, n-1) = 1$)
Siis myös tämän tapauksen luvuilla $n$ pätee $a_{n+s} \equiv a_n \pmod{p^k}$ kaikilla suurilla $n$.
- $p$ jakaa luvun $n-1$. Tämä tapaus on analoginen tapauksen 2 kanssa.
Tapauskäsittely osoittaa lemman 2. Lemmat 1 ja 2 yhdessä osoittavat, että kaikki $m$ kelpaavat.
Huomautus
Ratkaisuidea on luonnollinen: lemma 1 on hyvin yleinen idea, ja tällainen sievennys kannattaa usein tehdä. Lemman 2 todisuksen voi motivoida seuraavasti: Eulerin lause osoittaa, että $a^n$ on jaksollinen mod $m$, kun $a$ on luvun $m$ kanssa yhteistekijätön vakio. Tämä käsittelee tapauksen 1. Enää tulee tutkia tapausten 2 ja 3 mukaiset erikoistapaukset.
Huomaa, että yleisesti $a^n$ on jaksollinen jostain pisteestä lähtien mod $m$ kaikilla $a, m \in \mathbb{Z}$. Tämä on varsin tunnettua (ja helppo seuraus Eulerin lauseesta). Myös tätä kautta voi ratkaista tehtävän hieman eri tavalla kuin edellä.
Tehtävästä tekee hieman vaikeamman se, että pyydetään löytämään ne $m$, joilla väite pätee, eikä vain todistamaan, että kaikki $m$ kelpaavat. Tehtävää ratkoessani epävarmuutta toi se, etten nähnyt miksei jokin $m$ kelpaisi. Ajattelin siis, etten huomaa jotakin ilmeistä. Keksittyäni ratkaisun olin kuitenkin luottavainen sen toimivuuteen. Lopputuloksena kuusi pistettä.
Tehtävä 5
Ratkaisun idea on Roope Salmen.
Olkoon $a$ oppilaan $A$ saamien omenoiden määrä, ja $b$ $B$:n omenoiden määrä. Voimme esittää luvut $a$ ja $b$ binäärissä. Lisäksi tiedämme, että luvun $a+b = 2^k - 1$ binääriesitys sisältää $k$ kappaletta numeroa $1$. Tämä tarkoittaa, että niissä kohdissa, joissa luvussa $a$ on numero $1$, on luvussa $b$ numero $0$, ja toisin päin. Esimerkiksi jos $k = 5, a = 13, b = 18$, niin
ja
Tässä kannattaa ajatella $a$:ta merkkijonona $01101$, jossa on lisätty $0$ niin, että $a$ on yhtä pitkä kuin $b$.
Tehtävä palautuu siis seuraavaan muotoon: oppilailla $A$ ja $B$ on annettuna binäärimerkkijonot. Heidän tulee määrittää, kumman merkkijono on pidempi.
Idea on seuraava: määritellään binäärimerkkijonoille funktio $f$, jolle määritellään $f(s)$ binäärimerkkijonolle $s$ seuraavasti:
Käydään $s$:n numeroita alusta loppuun. Lasketaan niiden siirtymien määrä, joissa siirrymme eri numeroon kuin mistä tulimme. $f(s)$ määritellään näiden siirtymien määräksi.
Esimerkki: $f(11111100011) = 2$, koska muutosten määrä on $2$.
Lukujen $a$ ja $b$ ominaisuuksien nojalla pätee joko $f(b) = f(a) + 1$ (jos $b$ on pidempi kuin $a$, kuten esimerkissä $a=13$, $b=18$), $f(a) = f(b) + 1$ (jos $a$ on pidempi kuin $b$), tai $f(a) = f(b)$ (jos $k = 0$).
Oppilaat voivat viestittää luvun $f(s)$ modulo $3$ rapsuttamalla päätään sopivasti. On helppoa nähdä, että tämä antaa ratkaisun tehtävään.
Huomautus
Ratkaisu on elegantti, ja se mahdollistaa vielä vahvemmin, että ulkopuolinen oppilas $C$ voisi päätellä $A$:n ja $B$:n päänrapsutuksista enemmän omenia saaneen oppilaan, vaikkei $C$:llä itsellään ole mitään suoraa tietoa omenoista.
Ongelman tutkiminen binäärimerkkijonoina on luonnollista, ja omenoiden määrä $2^k - 1$ vihjaa tähän suuntaan. Keksin tämän idean, mutten keksinyt kriittistä ideaa muutosten määrän laskemisesta. Lopputuloksena yksi piste.